Scilabで波形解析の勉強中(単純移動平均によるノイズの平滑化)
- 2013/11/02
- 21:17
CQ出版社の「Scilab入門 (大川善邦著)」で勉強しています。工学的にもレベルの高い内容を簡便にまとめたとても良い本なのですが、初学者には途中が分かりづらいところも多く、苦労しました。個人的な防備録です。(この記事も端折っているところが多いことを承知していますが、個人的な防備録ということでご容赦願います。いつか丁寧に書き直せればと思います〕
仮にxに最後に添付したようなデータが代入されていたとします。
このxに対して単純にplotすると次の通りとなります。
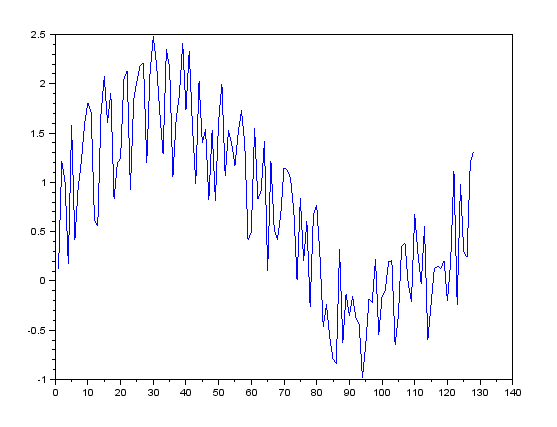
さて、このxに対して単純移動平均を使い、ノイズを平滑化してみましょう。次の式を使います。
まずこのscilabのスクリプトを読込みます。
-->exec('movave.sci')
そして単純移動平均を使って平滑化したデータをyおよびy2とします。それぞれ、スパンを1と3として、平滑化しています。
最終的にx、yおよびy2を重ねてplotしてみましょう。分かりやすいように色を変えています。
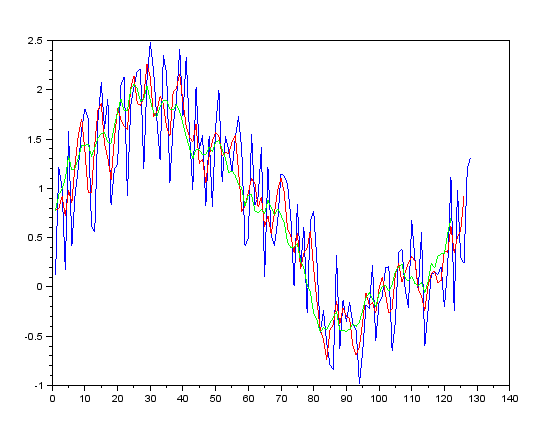
いかがでしょう。このようにもともとのノイズが平滑化されていく様子が分かると思います。
-->x
x =
0.1264897
1.2129952
1.0036602
0.1729712
1.5782405
0.4174043
0.9388323
1.2149275
1.6000938
1.8087148
1.7028309
0.6147606
0.5568364
1.6944389
2.0721791
1.608637
1.9073498
0.8274307
1.1922035
1.248821
2.0435278
2.1330404
0.9264366
1.8342634
2.0288983
2.1875188
2.2077628
1.1990715
2.1063092
2.479181
2.1946336
1.7015175
1.2910821
2.345001
2.1686946
1.0549354
1.6415012
1.8936499
2.4144687
1.7341093
2.3342741
1.5551764
0.9906141
2.0238292
1.400569
1.5377264
0.8224160
1.5273907
0.8184764
1.6268398
1.9968465
1.0661916
1.522688
1.3923442
1.1693609
1.5086416
1.7246005
1.3852612
0.4135782
0.4977468
1.5468636
0.8303553
0.9147481
1.4109466
0.1027075
1.213852
0.5256967
0.4246119
0.6704330
1.1481728
1.127669
1.0395627
0.7132832
0.0062328
0.8399817
0.2014862
0.6045971
- 0.2585392
0.6779304
0.7655637
0.2567430
- 0.4638138
- 0.2407652
- 0.5779273
- 0.7885088
- 0.8389518
0.3232153
- 0.6311532
- 0.1317764
- 0.35279
- 0.1574515
- 0.3789825
- 0.4373964
- 0.9820469
- 0.6562250
- 0.1807200
- 0.2197603
0.2198833
- 0.5447156
- 0.1595177
- 0.0951699
0.1972291
0.2044302
- 0.6498597
- 0.3569228
0.3518487
0.3867190
- 0.0233764
- 0.2070345
0.6741294
0.2762051
- 0.0304471
0.5493576
- 0.6010724
- 0.2336461
0.1226762
0.1503910
0.1267047
0.2057953
- 0.2009539
0.1940034
1.1100968
- 0.2468777
0.9820300
0.2959132
0.2379027
1.1986828
1.315955
仮にxに最後に添付したようなデータが代入されていたとします。
このxに対して単純にplotすると次の通りとなります。
-->plot(x)

さて、このxに対して単純移動平均を使い、ノイズを平滑化してみましょう。次の式を使います。
movave.sci
function [y, q]=movave(x,m)
n=length(x)
y=zeros(1:n-2*m)
q=0
for i=1:n-2*m
for j=1:2*m+1
y(i)=y(i)+x(i+j-1)
end
y(i)=y(i)/(2*m+1)
q=q+abs(x(i+m)-y(i))
end
q=q/(n-2*m)
endfunction
まずこのscilabのスクリプトを読込みます。
-->exec('movave.sci')
そして単純移動平均を使って平滑化したデータをyおよびy2とします。それぞれ、スパンを1と3として、平滑化しています。
-->y=movave(x,1)
-->y2=movave(x,3)
最終的にx、yおよびy2を重ねてplotしてみましょう。分かりやすいように色を変えています。
-->plot(x)
-->plot(y,'r')
-->plot(y2,'g')

いかがでしょう。このようにもともとのノイズが平滑化されていく様子が分かると思います。
-->x
x =
0.1264897
1.2129952
1.0036602
0.1729712
1.5782405
0.4174043
0.9388323
1.2149275
1.6000938
1.8087148
1.7028309
0.6147606
0.5568364
1.6944389
2.0721791
1.608637
1.9073498
0.8274307
1.1922035
1.248821
2.0435278
2.1330404
0.9264366
1.8342634
2.0288983
2.1875188
2.2077628
1.1990715
2.1063092
2.479181
2.1946336
1.7015175
1.2910821
2.345001
2.1686946
1.0549354
1.6415012
1.8936499
2.4144687
1.7341093
2.3342741
1.5551764
0.9906141
2.0238292
1.400569
1.5377264
0.8224160
1.5273907
0.8184764
1.6268398
1.9968465
1.0661916
1.522688
1.3923442
1.1693609
1.5086416
1.7246005
1.3852612
0.4135782
0.4977468
1.5468636
0.8303553
0.9147481
1.4109466
0.1027075
1.213852
0.5256967
0.4246119
0.6704330
1.1481728
1.127669
1.0395627
0.7132832
0.0062328
0.8399817
0.2014862
0.6045971
- 0.2585392
0.6779304
0.7655637
0.2567430
- 0.4638138
- 0.2407652
- 0.5779273
- 0.7885088
- 0.8389518
0.3232153
- 0.6311532
- 0.1317764
- 0.35279
- 0.1574515
- 0.3789825
- 0.4373964
- 0.9820469
- 0.6562250
- 0.1807200
- 0.2197603
0.2198833
- 0.5447156
- 0.1595177
- 0.0951699
0.1972291
0.2044302
- 0.6498597
- 0.3569228
0.3518487
0.3867190
- 0.0233764
- 0.2070345
0.6741294
0.2762051
- 0.0304471
0.5493576
- 0.6010724
- 0.2336461
0.1226762
0.1503910
0.1267047
0.2057953
- 0.2009539
0.1940034
1.1100968
- 0.2468777
0.9820300
0.2959132
0.2379027
1.1986828
1.315955
0 件のコメント:
コメントを投稿