※ Scilabを使っていますが、ソースコードを掲載することはMatlabのFile Exchangeの規約に反すると思われ、掲載を見送っています。いつかオリジナルでプログラミングした際に、ソースコードを掲載したいと思います。
以前、あるドクターから宿題があり、FDTDによる電磁波伝播のシミュレーションの勉強をしたことがあります。
その際にMatlabクローンのScilabを使って、自由空間を1次元方向に進む電磁波をシミュレーションしてみたのが、下記のグラフです。
原点(0,0,0)で時間的にSineとして振動する電場を与え、それが垂直方向に磁場を作り、またその磁場が電場を作っていきます。実際はこの波が進んでいく様子が 経時的にアニメーションのように表示されます。
2014年11月23日日曜日
付録:グラフのお化粧およびアニメーションの作成 : 最終のScilabコード(1)
※ ソースコードを見やすくするために、Syntaxhilighterを使っています。状況によって表示に時間がかかる場合があります。
前回Sine波を重ね合わせてのこぎり波を近似するプログラムを前回紹介しました。
Scilabにおける関数の定義と使い方(2)
波形を表示するエッセンスの部分は非常に短いコードですが、グラフのタイトルや軸の名称がなかったり、表示ごとに縦軸の最大値が表示波形の振幅に伴って変わってしまうなど問題が残っています。
その際エッセンスの部分のコードだけ紹介しましたが、グラフのフォーマットなどを含めた最終的なものをご参考に記載します。最後に描かせたグラフを静止画のgifフォーマットとして出力させています。
前回Sine波を重ね合わせてのこぎり波を近似するプログラムを前回紹介しました。
Scilabにおける関数の定義と使い方(2)
波形を表示するエッセンスの部分は非常に短いコードですが、グラフのタイトルや軸の名称がなかったり、表示ごとに縦軸の最大値が表示波形の振幅に伴って変わってしまうなど問題が残っています。
その際エッセンスの部分のコードだけ紹介しましたが、グラフのフォーマットなどを含めた最終的なものをご参考に記載します。最後に描かせたグラフを静止画のgifフォーマットとして出力させています。
2014年9月7日日曜日
付録:グラフのお化粧およびアニメーションの作成 : 最終のScilabコード (2)
※ ソースコードを見やすくするために、Syntaxhilighterを使っています。状況によって表示に時間がかかる場合があります。
後日追記
ImageMagicを使ったGifアニメーションはループになっていなかったので、最終的にはAdobeのFlashを使いました。アニメに出力した際グラフの線が途切れ途切れになってしまい苦労しました。画像サイズをFlash上で変えないほうが良いようです。
前回の続きです。
最後にGifファイルをつないでアニメーションを作る方法です。Webを調べ、ImageMagicというオープンソフトを使うとできることがわかりました。
後日追記
ImageMagicを使ったGifアニメーションはループになっていなかったので、最終的にはAdobeのFlashを使いました。アニメに出力した際グラフの線が途切れ途切れになってしまい苦労しました。画像サイズをFlash上で変えないほうが良いようです。
************************************************************
前回の続きです。
付録:グラフのお化粧およびアニメーションの作成 : 最終のScilabコード(1)
最後にGifファイルをつないでアニメーションを作る方法です。Webを調べ、ImageMagicというオープンソフトを使うとできることがわかりました。
MatlabプログラムをScilabに変換、再編集するに当たって
Scilabのコードは大雑把な言い方ですが、90%程度Matlabと同じです。コツさえつかめれば、Matlabの簡単なコードをScilab上で動かすことはさほど時間が掛かりません。
もちろん複雑なコードはそれなりに時間が掛かったり、落とし穴があって悩んだりしますが。
ポイントは次の通りです。私は付属のSciNotesをエディタとして使っていますが、Find & Replaceが活躍します。
もちろん複雑なコードはそれなりに時間が掛かったり、落とし穴があって悩んだりしますが。
ポイントは次の通りです。私は付属のSciNotesをエディタとして使っていますが、Find & Replaceが活躍します。
2014年9月6日土曜日
Scilabにおける関数の定義と使い方(2)
※ ソースコードを見やすくするために、Syntaxhilighterを使っています。状況によって表示に時間がかかる場合があります。
今回もC/C++を勉強していた時のテキストブックに出ていたプログラムをScilabで作ってみました。
関数の定義には、多少ですが、前回とは違う方法があり、これを使いました。
関数形は下記より調べ、k=11まで重ね合わせて作成したものが下のアニメーションです。kの数を増やしていくとさらにきれいなのこぎり波となっていきます。
Wiki: のこぎり波
今回もC/C++を勉強していた時のテキストブックに出ていたプログラムをScilabで作ってみました。
関数の定義には、多少ですが、前回とは違う方法があり、これを使いました。
倍音としてSine波を徐々に重ね合わせていくとのこぎり波に近づいていく様子が分かると思います。
関数形は下記より調べ、k=11まで重ね合わせて作成したものが下のアニメーションです。kの数を増やしていくとさらにきれいなのこぎり波となっていきます。
Wiki: のこぎり波
Scilabにおける関数の定義と使い方(1)
今回はC/C++を勉強していた時のテキストブックに出ていたプログラムをScilabで作ってみました。
まずは関数の定義のしかたと使い方を習得するために階乗のプログラムです。ここではForループでも良かったのですが、whileループとしました。
Scilab自体にfactorial()という関数があるので、ここではmyFactorialという関数名としました。引数を一つとり、この引数(int型)の階乗を計算してその値を返します。
Scilabのヘルプにも関数の使い方は載っており、参考としました。
14行目はデバックの目的で入れてあります。5の階乗を計算させていますが、ループが正しく回っていることがコンソール画面上で確認できます。
まずは関数の定義のしかたと使い方を習得するために階乗のプログラムです。ここではForループでも良かったのですが、whileループとしました。
Scilab自体にfactorial()という関数があるので、ここではmyFactorialという関数名としました。引数を一つとり、この引数(int型)の階乗を計算してその値を返します。
Scilabのヘルプにも関数の使い方は載っており、参考としました。
14行目はデバックの目的で入れてあります。5の階乗を計算させていますが、ループが正しく回っていることがコンソール画面上で確認できます。
Scilab ― 始めの一歩と免責事項
むかしMathematicaという数値計算ソフトをかじっていましたが、恥ずかしながら十分に使いこなしてはいませんでした。
今回数値シミュレーションを勉強するに当たってMatlabクローンであるScilabを選びました。
今回数値シミュレーションを勉強するに当たってMatlabクローンであるScilabを選びました。
2014年6月1日日曜日
Scilabで波形解析の勉強中(フーリエ変換)
前回に続いて、これも防備録です。CQ出版社の「Scilab入門 (大川善邦著)」の第4章フーリエ変換です。
次のグラフはノイズをのせたSin波形とそのFFTのグラフです。後述のスクリプトの最後の方にありますが、n=32としています。
次のグラフはノイズをのせたSin波形とそのFFTのグラフです。後述のスクリプトの最後の方にありますが、n=32としています。
n=2とn=30で同じピークになっていますが、これがナイキストの定理を視覚化したものだろうと思います。
まずはシンプルに4点でFFTをかけてみます。
-->x=[0:3]
-->y=[1 2 -3 1]
-->F=fft(y)
-->plot(x,abs(F))
-->atan(imag(F)/real(F))
-->plot(x,F)
次に32点に拡張してみます。
-->n=32
-->x=[0:n-1]
Cos波形です。m=1としています。
-->m=1
-->yc=cos(2*%pi/n*m*x)
-->plot(x,yc)
Sin波形です。今度はm=2としています。
-->m=2
-->ys=sin(2*%pi/n*m*x)
-->plot(x,ys)
Sin波形にノイズを乗っけてみます。
-->ysr=ys+0.5*(rand(x)-0.5)
-->plot(x,ysr)
-->fsr=fft(ysr)
-->plot(fsr)
-->plot(x,abs(fsr))
※ ソースコードを見やすくするために、Syntaxhilighterを使っています。状況によって表示に時間がかかる場合があります。
Scilabで波形解析の勉強中(単純移動平均によるノイズの平滑化)
- 2013/11/02
- 21:17
CQ出版社の「Scilab入門 (大川善邦著)」で勉強しています。工学的にもレベルの高い内容を簡便にまとめたとても良い本なのですが、初学者には途中が分かりづらいところも多く、苦労しました。個人的な防備録です。(この記事も端折っているところが多いことを承知していますが、個人的な防備録ということでご容赦願います。いつか丁寧に書き直せればと思います〕
仮にxに最後に添付したようなデータが代入されていたとします。
このxに対して単純にplotすると次の通りとなります。
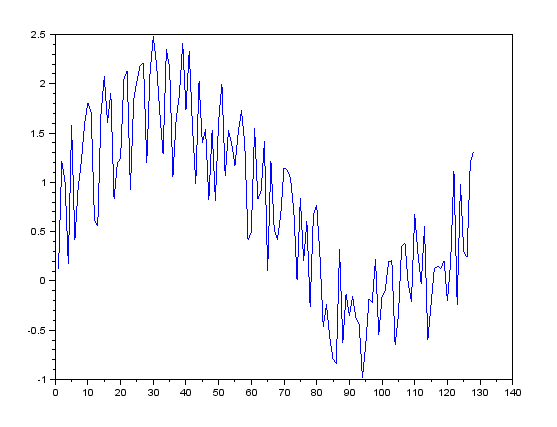
さて、このxに対して単純移動平均を使い、ノイズを平滑化してみましょう。次の式を使います。
まずこのscilabのスクリプトを読込みます。
-->exec('movave.sci')
そして単純移動平均を使って平滑化したデータをyおよびy2とします。それぞれ、スパンを1と3として、平滑化しています。
最終的にx、yおよびy2を重ねてplotしてみましょう。分かりやすいように色を変えています。
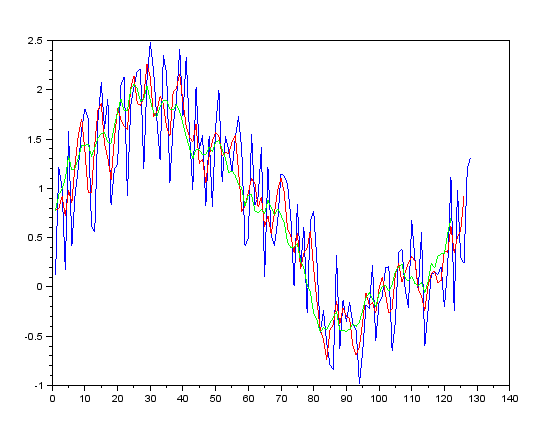
いかがでしょう。このようにもともとのノイズが平滑化されていく様子が分かると思います。
-->x
x =
0.1264897
1.2129952
1.0036602
0.1729712
1.5782405
0.4174043
0.9388323
1.2149275
1.6000938
1.8087148
1.7028309
0.6147606
0.5568364
1.6944389
2.0721791
1.608637
1.9073498
0.8274307
1.1922035
1.248821
2.0435278
2.1330404
0.9264366
1.8342634
2.0288983
2.1875188
2.2077628
1.1990715
2.1063092
2.479181
2.1946336
1.7015175
1.2910821
2.345001
2.1686946
1.0549354
1.6415012
1.8936499
2.4144687
1.7341093
2.3342741
1.5551764
0.9906141
2.0238292
1.400569
1.5377264
0.8224160
1.5273907
0.8184764
1.6268398
1.9968465
1.0661916
1.522688
1.3923442
1.1693609
1.5086416
1.7246005
1.3852612
0.4135782
0.4977468
1.5468636
0.8303553
0.9147481
1.4109466
0.1027075
1.213852
0.5256967
0.4246119
0.6704330
1.1481728
1.127669
1.0395627
0.7132832
0.0062328
0.8399817
0.2014862
0.6045971
- 0.2585392
0.6779304
0.7655637
0.2567430
- 0.4638138
- 0.2407652
- 0.5779273
- 0.7885088
- 0.8389518
0.3232153
- 0.6311532
- 0.1317764
- 0.35279
- 0.1574515
- 0.3789825
- 0.4373964
- 0.9820469
- 0.6562250
- 0.1807200
- 0.2197603
0.2198833
- 0.5447156
- 0.1595177
- 0.0951699
0.1972291
0.2044302
- 0.6498597
- 0.3569228
0.3518487
0.3867190
- 0.0233764
- 0.2070345
0.6741294
0.2762051
- 0.0304471
0.5493576
- 0.6010724
- 0.2336461
0.1226762
0.1503910
0.1267047
0.2057953
- 0.2009539
0.1940034
1.1100968
- 0.2468777
0.9820300
0.2959132
0.2379027
1.1986828
1.315955
仮にxに最後に添付したようなデータが代入されていたとします。
このxに対して単純にplotすると次の通りとなります。
-->plot(x)

さて、このxに対して単純移動平均を使い、ノイズを平滑化してみましょう。次の式を使います。
movave.sci
function [y, q]=movave(x,m)
n=length(x)
y=zeros(1:n-2*m)
q=0
for i=1:n-2*m
for j=1:2*m+1
y(i)=y(i)+x(i+j-1)
end
y(i)=y(i)/(2*m+1)
q=q+abs(x(i+m)-y(i))
end
q=q/(n-2*m)
endfunction
まずこのscilabのスクリプトを読込みます。
-->exec('movave.sci')
そして単純移動平均を使って平滑化したデータをyおよびy2とします。それぞれ、スパンを1と3として、平滑化しています。
-->y=movave(x,1)
-->y2=movave(x,3)
最終的にx、yおよびy2を重ねてplotしてみましょう。分かりやすいように色を変えています。
-->plot(x)
-->plot(y,'r')
-->plot(y2,'g')

いかがでしょう。このようにもともとのノイズが平滑化されていく様子が分かると思います。
-->x
x =
0.1264897
1.2129952
1.0036602
0.1729712
1.5782405
0.4174043
0.9388323
1.2149275
1.6000938
1.8087148
1.7028309
0.6147606
0.5568364
1.6944389
2.0721791
1.608637
1.9073498
0.8274307
1.1922035
1.248821
2.0435278
2.1330404
0.9264366
1.8342634
2.0288983
2.1875188
2.2077628
1.1990715
2.1063092
2.479181
2.1946336
1.7015175
1.2910821
2.345001
2.1686946
1.0549354
1.6415012
1.8936499
2.4144687
1.7341093
2.3342741
1.5551764
0.9906141
2.0238292
1.400569
1.5377264
0.8224160
1.5273907
0.8184764
1.6268398
1.9968465
1.0661916
1.522688
1.3923442
1.1693609
1.5086416
1.7246005
1.3852612
0.4135782
0.4977468
1.5468636
0.8303553
0.9147481
1.4109466
0.1027075
1.213852
0.5256967
0.4246119
0.6704330
1.1481728
1.127669
1.0395627
0.7132832
0.0062328
0.8399817
0.2014862
0.6045971
- 0.2585392
0.6779304
0.7655637
0.2567430
- 0.4638138
- 0.2407652
- 0.5779273
- 0.7885088
- 0.8389518
0.3232153
- 0.6311532
- 0.1317764
- 0.35279
- 0.1574515
- 0.3789825
- 0.4373964
- 0.9820469
- 0.6562250
- 0.1807200
- 0.2197603
0.2198833
- 0.5447156
- 0.1595177
- 0.0951699
0.1972291
0.2044302
- 0.6498597
- 0.3569228
0.3518487
0.3867190
- 0.0233764
- 0.2070345
0.6741294
0.2762051
- 0.0304471
0.5493576
- 0.6010724
- 0.2336461
0.1226762
0.1503910
0.1267047
0.2057953
- 0.2009539
0.1940034
1.1100968
- 0.2468777
0.9820300
0.2959132
0.2379027
1.1986828
1.315955
登録:
投稿 (Atom)



